Library for IMC's Mock Trading

!pip install cardquant

Disclaimer: Any firms, people, or events mentioned—even those that sound eerily familiar—are entirely fictional. Any resemblance to anything in real life is purely coincidental. My blog is written…poorly.

Last summer, a Reddit user revealed IMC’s mock trading game for interns—no names, but it rhymes with ‘drive a car’. The post had two key takeaways: first, IMC’s mock trading blueprint is now out in the open; second, IMC interns apparently think DP stands for “Don’t Program.”

I’m here to save the day—since apparently I have nothing better to do with my free time than crank out random side projects—by building a library so IMC interns can just worry about quote placement and position management while I quietly handle theos, greeks, and all that arcane math.

Rules

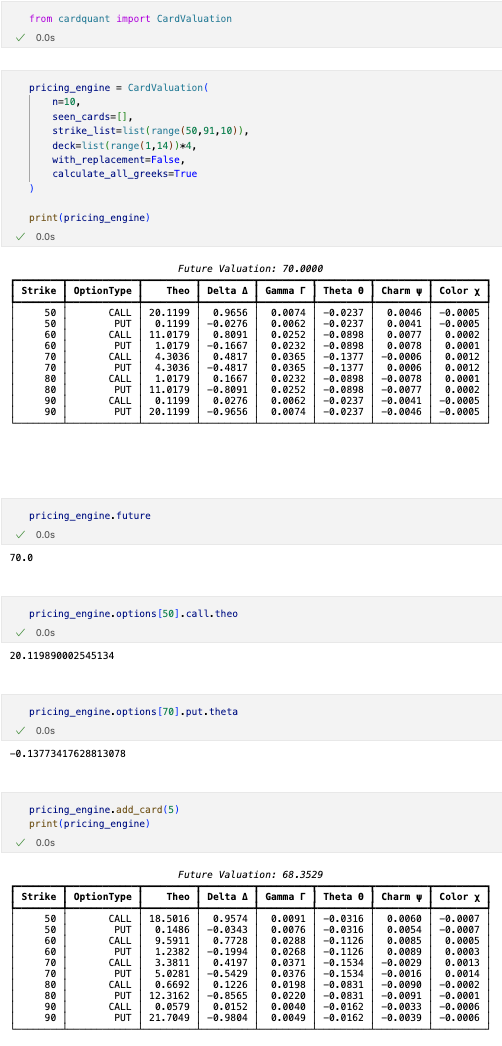
In this simulation, 10 cards are drawn one by one without replacement from a standard 52-card deck. Each card is assigned a value from 1 to 13 (Ace = 1, …, King = 13). A “future” contract settles to the sum of the 10 cards. Call options settle to max(0, future - strike) and puts will settle to max(0, strike - future) for strikes at 50, 60, 70, 80, and 90. While the defaults mirror the original Reddit post, the library is built to be able to adapt if the rules ever change.

Installing the Library

pip install cardquant

Usage

Instant Calculations & Access

Thanks to dynamic programming, all theoretical values and Greeks are computed virtually instantly once an instance is created. You can access results directly:

• Future sum: instance.future

• Call option Theo: instance.options[strike].call.theo

• Call option Delta: instance.options[strike].call.delta

• Put option Theo: instance.options[strike].put.theo

• Put option Delta: instance.options[strike].put.delta

Note that the same methodology for accessing delta is used for all other greeks (assuming calculate_all_greeks is set to True).

Printing the instance will display a formatted table with all strikes, Theos, and Greeks.

The parameters shown above are the default values; they’re included here for illustration—feel free to customize them when you instantiate your own.

Adaption/Modification of Standard Options Greeks

• Delta (Δ)

  • Call: Δ_call(K) = P(future > K)

  • Put: Δ_put(K) = −P(future < K)
    Note: If P(future = K) > 0 then |Δ_call| + |Δ_put| will be less than 1.

• Gamma (Γ)
  Discrete rate of change of Delta with respect to strike:

  \(\Gamma(K)\approx\frac{\Delta(K+1)-\Delta(K-1)}{2}\)

• Theta (Θ)
  Sensitivity of Theo to drawing one more card at its expected value. Let:

  1. EV = mean of remaining cards

  2. floor = ⌊EV⌋, ceil = ⌈EV⌉

  3. f_w = (ceil - EV) / (ceil - floor), c_w = (EV - floor) / (ceil - floor)

     \(\Theta(K) = \bigl[\mathrm{Theo}({\text{current + floor}})\cdot f_{w} + \mathrm{Theo}({\text{current + ceil}})\cdot c_w\bigr] - \mathrm{Theo}(\text{current})\)

  If one of the discrete values (floor or ceil) has no remaining cards, shift to the next available value and adjust weights (f_w and c_w) accordingly.

• Charm (ψ)
  Rate of change of Delta under the same EV interpolation used for Theta:

• Color (χ)
  Rate of change of Gamma under the same EV interpolation:

Note: Greeks tied to volatility (e.g., Vega, Volga) aren’t meaningful in the context of this game.

Good Luck!

If you see any improvements to be made (and/or oversights on my part), feel free to commit your changes¹. Like I said before, I don’t have anything better to do with my free time, so I’ll be able to review anything pushed.

1. https://github.com/evansemet/cardquant