Hedging in Part
why fully hedging deltas is suboptimal even under concave utility
Disclaimer: I am not a financial advisor. I’m a blueberry. I possess no formal financial education, no advanced degrees, and possibly no brain cells. I am merely a moron with a Substack. Absolutely nothing in this article is truthful, factual, or even remotely accurate—it is pure, unfiltered parody. While I will reference various complex concepts, I will simplify them to a level that makes sense to me, which means they will become entirely nonsensical and wrong. Please do not take anything in this article seriously or as advice. I am making all of this up. None of it is true. Not a single word.
Overview
I’m first going to walk through a really simple example, then go through some more formal utility theory, and finally wrap up with an application to options trading.
TLDR: Never fully hedge unless the hedge is truly >= 0 EV.
Kalshi/Polymarket Price Discrepancy
I saw a ton of posts about how there was about a 2% arbitrage between Mamdani’s odds on Kalshi and Polymarket (even after accounting for crossing spreads + fees). Was the arb even that good of a trade? Yes. 2% risk free (let’s fully discount some exchange FTX scenario) on a single trade is pretty bonkers.
Note: the interest for the positions is different (Kalshi has interest for all positions and resting cash in the account) and also the ‘holdup’ period was different as Kalshi’s contracts went until he was sworn in; we are ignoring this ‘time value of money’ component.
Now if you were able to idk read the room at all, you would’ve known that there was practically 0 chance that Cuomo was going to win. The only real scenario in which that could have happened was if Silwa dropped out AND 100% of his voters voted for Cuomo and then he still would have only had a fighting chance. This was not happening. Just because maybe my ability to properly estimate these tail events is not amazing (it hasn’t been battle tested), let’s assume that Silwa dropping out was a 2% chance and in 100% of these scenarios it’s a coin toss between Mamdani and Cuomo giving Mamdani a 99% chance of winning.
Note: Bill Ackman would’ve strongly disagreed with this and probably still insists that he was right, but I could also care less about his analysis on this sort of stuff (or many other things for that matter).
Now let’s say that you could buy Mamdani YES on Kalshi for 92c and Mamdani NO on Polymarket for 6c, what do you do? Do you buy both for 98c and lock in the 2c of arb for just over a 2% risk free profit (2/98 > 2%)? Do you only do the more +EV leg? Maybe some combination? Well ultimately it comes down to your utility function, but suppose that you have a utility function that is both increasing and concave, like ln(w) utility or something, then you should not hedge the full amount; there should be some amount of risk that you are willing to take to increase your expectancy. Even if this means you have ratios of contracts set up in a way such that you just don’t lose money on a Mamdani loss, but make on a Mamdani win.
I leave it to the reader to set up the equation for ratios to only have upside in a Mamdani win and other optimization based upon your utility function. I think that this sort of distracts from this post as this should serve to teach about the thought process for trading, not how to use scipy.optimize. Anyway, read the rest of the post before you think about what is ideal here (if it’s not already obvious to you).
Kalshi/Polymarket Arbitrage
This probably doesn’t need its own section, but I think it deserved it’s own title because it’s really important. Suppose you are an uniformed participant and don’t actually know how to figure out some rough odds of a candidate winning. You should just do the arbitrage. You have no way of knowing which is the +EV leg or calculating EV at all for that matter.
Note: This happens a lot in crypto. There can be major price discrepancies across exchanges for coins on super volatile days and the best trade for a normally knowledgeable trader is just to do the arb because you really have no idea where anything is going to end up when the dust settles.
The Optimal Insurance has a Deductible
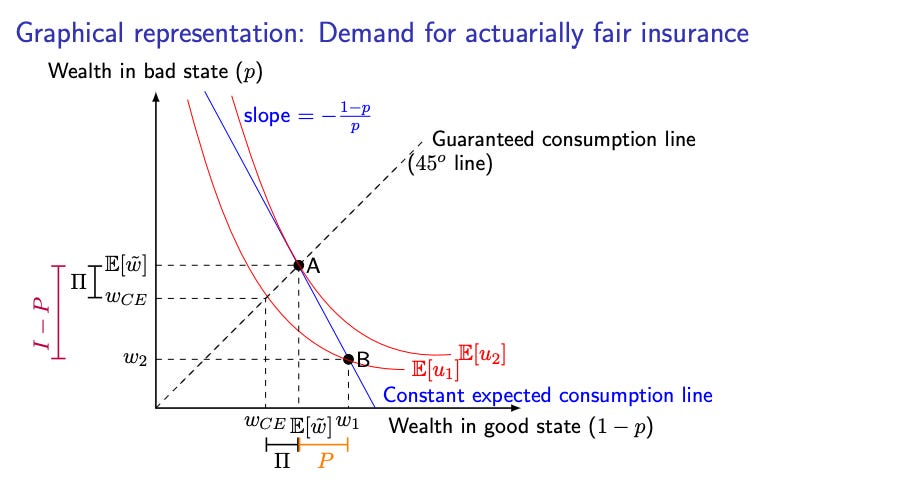
I think it’s pretty intuitive why, but if insurance was actuarily fair (it trades at its EV), then you would insure the full amount. It is a strict decrease in variance (and higher moments too) for no change in expectation, which increases utility for any increasing, concave utility function.
I feel like these types of diagrams are a little easier to read if you’ve taken some economics classes before, but hopefully you can see that we move to a strictly higher utility curve under full insurance.
Now let’s dive into some utility theory here for a bit. Let’s say that we have some loading cost lambda > 0, such that the price for the insurance is (1 + lambda) * EV of the insurance. Just to make sure we’re on the same page, if lambda is 0.05, that means that the insurance costs 5% more than its expected value.
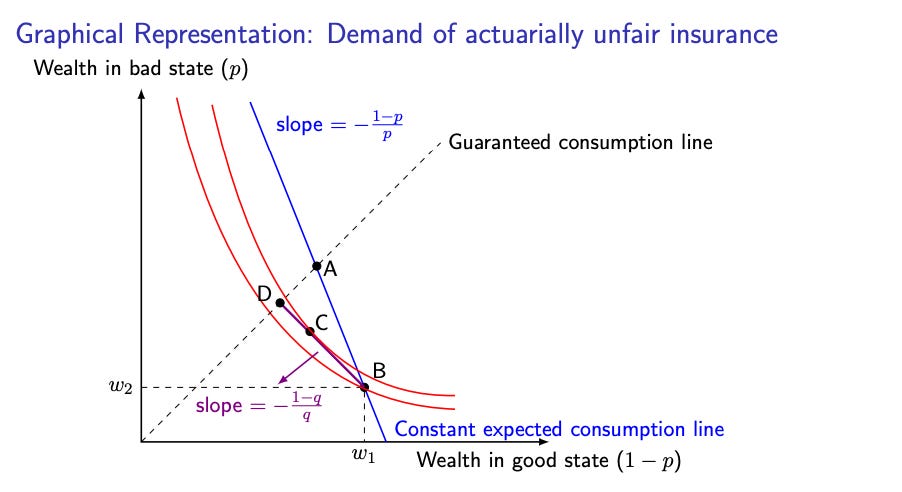
If lambda is too high, then there is no amount of insurance that you would purchase. Let’s think about some extreme cases here: if it costs more to insure your house than the house is worth, you clearly would not insure it; if it costs almost as much as the house to insure it then you would also not insure it.
I’m not exactly sure what the demographics of my readers are, but hopefully you know at least something about health insurance. I would wager that most of the readers reading this are not able to front a several million dollar hospital bill in the case of some freak accident? For most people, that would be pretty catastrophic. There are some people that can weather through stuff like a broken wrist or some other not minor, but not necessarily major, hospital bill. Anyway, if insurance gets too expensive, people start to gravitate towards only purchasing catastrophic insurance. In other words, they only partially insure themselves.
Because there is typically some amount of variance that people are willing to take on, they are not willing to take a loss in expected value to remove 100% of variance. Maybe this is easier to reason through for the case of insurance on small things like idk a toaster. If you buy a toaster for 20 dollars, do you really feel the need to purchase toaster insurance? probably not. Likewise, stuff like Apple Care doesn’t make sense for those with enough money where the Apple product they bought is analogous to the toaster with respect to their net worth/level of risk aversion.
So with a non-zero loading cost, there is some amount you do not need to fully insure. If you are fine not insuring a 20 dollar toaster, then logically speaking you should be fine insuring all but like 20 dollars of your house right? (You are almost certainly fine not insuring a larger percentage of your house, but I like to use extremes/limits for examples.) If we ignore the moral hazard1 component of insurance, we can see that from a pure utility optimization perspective, insurance companies having a deductible equal to the amount that one would choose to not insure (if there was a granular percentage insurance ability) is ideal; insurance having a deductible is actually something that is very well supported mathematically.
Hedging Deltas
First and foremost, options are NOT var swaps. When you buy an option, you are not just expressing a view on volatility, you have a delta opinion (or bias at least) and a volatility view. I think it’s also important to recognize that when you hedge your option deltas, you are actively driving the underlying in the wrong direction. For example, if you just bought call options, and start selling the underlying, you will have some non zero impact on lowering the price of the underlying and thus adding at least some negative delta quality to the purchase of those aforementioned call options. This is an insignificant amount for retail purchasing highly liquid options, but is something that 100% matters for trading firms.
Even if we completely ignore trading fees on the underlying, the mere fact that hedging with the underlying hurts the delta component of your own option should suffice to show that hedging the underlying for “fair” actually has some negative expectancy to it. When you factor in transaction fees, this negative expectancy strictly increases. Normally options are seen as the “insurance”, but in this case where the option view is the actual trade, the underlying is the “insurance” for this. We have established how the underlying has some non zero lambda value associated with it and therefore it doesn’t make sense to fully hedge your deltas, but it (probably) makes sense to at least partially hedge them.
A lot of firms will have some hard caps on risk limits for different greeks (exposures). Suppose that your firm has a hard cap of an absolute delta exposure of X (where they allow a residual delta exposure within this +/- X price band), then as soon as you exceed this price band, you should only hedge your deltas to be within the price band—nothing more. If you are comfortable with up to an absolute value of X delta exposure, then why would you pay additional to bring it to zero? These delta bands can be seen as analogous to the “deductible” that is optimal for you. At a minimum, hedging to zero is logically inconsistent behavior; at the maximum, it is negative utility behavior.
Note: Technically you could bring it to zero (or even beyond) if you had the idea that there was some longer term delta toxicity of your options counterparty, but that’s not really what we are talking about because that would imply a lambda < 0 in that case and we are only talking about insurance with lambda > 0.
Back to Mamdani
If you have a view on which leg is +EV, can you now see why only a partial hedge is optimal? Hopefully I was able to draw parallels to hedge legs in trading and the deductible of insurance to show why full hedges aren’t ideal. Risk adds negative utility (for those with concave utility), but there should be some amount of risk you are willing to take if it means increasing your total expectancy.


Your previous post had more interesting links to readings. Please try to include even more, it looked sophisticated. Furthermore, I read them.