Face Value

The frequency factor

Let’s play a game… We’re going to roll a d3 (a fair, 3-sided die) 20 times, record the frequencies that each face value that shows up and take the product of said frequencies. What’s the expected value of such a game?

Just to make sure we’re on the same page here, an example simulation could end with six 1s, five 2s, and nine 3s giving this a value of 6 x 5 x 9 = 270.

First Thoughts:

Obviously the lower bound would have to be zero—if and if there is at least one face that does not appear during the 20 rolls. Albeit this is very rare. This is maximized when the frequencies are closest to the expectancy of the frequency of an individual appearance which would be ~ 20/3 for each, or more precisely, 7,7,6 as the frequencies leading to a value of 294. This is also the set of frequencies to appear most often so our actual expectancy should be fairly heavily skewed towards this value.

Mathing it out:

First things first, we can clearly see that this is a multinomial distribution where all probabilities are equal to 1/3. Let X_1,X_2,X_3 be the triple representing the frequencies for each respective face for n=20.

\(E[X_1X_2X_3] = \sum_{x_1=0}^{n}E[x_1X_2X_3|X_1=x_1]P(X_1=x_1)\)

\(= \sum_{x_1=0}^{n}E[X_2X_3|X_1=x_1]x_1P(X_1=x_1)\)

We also know that X_1 follows a binomial distribution with p=1/3 since we can think of this as X_1 or not X_1 for each independent roll.

\(P(X_1=x_1)= {n\choose x_1}\frac{1}{3}^{x_1}\frac{2}{3}^{n-x_1}\)

Similarly, X_2 and X_3 can be binomial with n → n - x_1 because conditioned on the roll being either X_1 or X_2, it is one of the two with p=1/2 as, by symmetry, they are equally likely. Let Y ~ Binomial(m, 1/2), what is E[Y(m-Y)]?

\(E[Y(m-Y)]=mE[Y]-E[Y^2]\)

\(Var(Y)=E[Y^2]-E[Y]^2\)

\(E[Y(m-Y)]=mE[Y]-Var(Y)-E[Y]^2\)

Trivially, E[Y]=m/2 and Var(Y)=m/4

\(E[Y(m-Y)]=m(\frac{m}{2})-\frac{m}{4}-\frac{m^2}{4}\)

\(E[Y(m-Y)]=\frac{m(m-1)}{4}\)

Now we can start to plug this back into our original

\(E[X_2X_3|X_1=x_1]=\frac{(n-x_1)(n-x_1-1)}{4}\)

\(E[X_1X_2X_3] = \sum_{x_1=0}^{n}\frac{(n-x_1)(n-x_1-1)}{4}x_1{n \choose x_1}\frac{1}{3}^{x_1}\frac{2}{3}^{n-x_1}\)

Lastly, this is 0 whenever one or more of the faces does not appear at all so we can reduce the summation bounds to:

\(E[X_1X_2X_3] = \sum_{x_1=1}^{n-2}\frac{(n-x_1)(n-x_1-1)}{4}x_1{n \choose x_1}\frac{1}{3}^{x_1}\frac{2}{3}^{n-x_1}\)

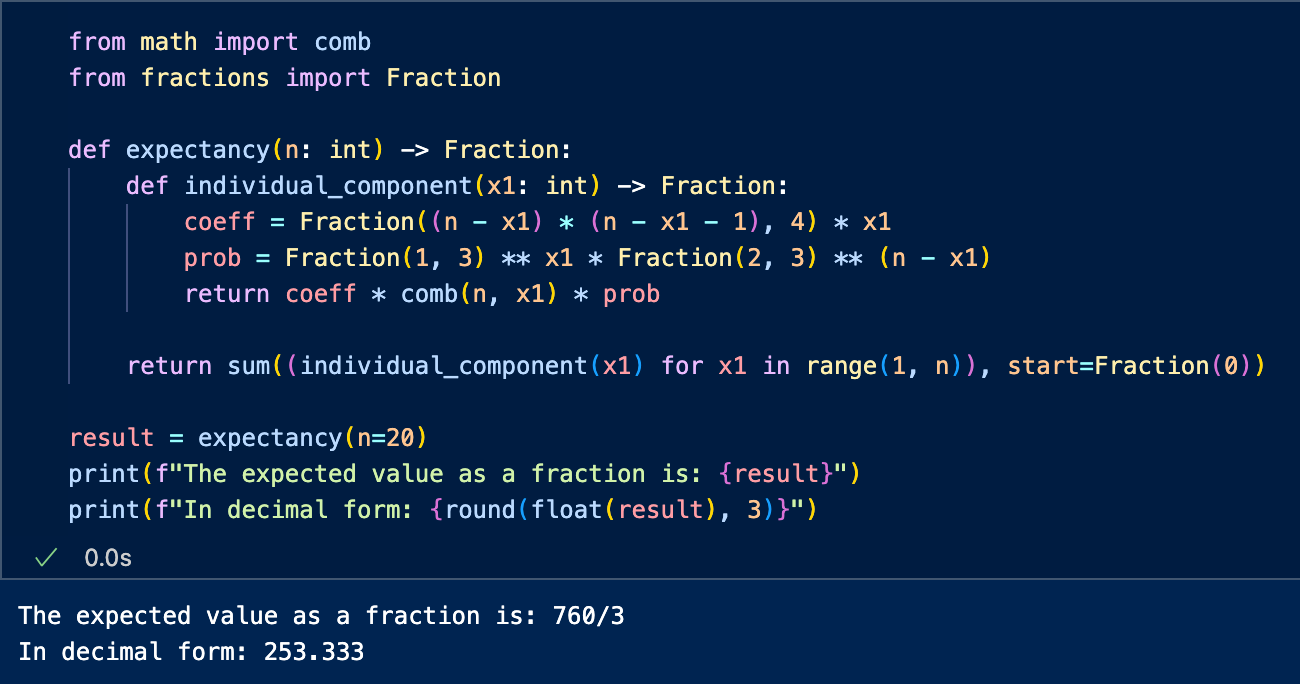
Using Code to Compute:

Exercise for the Reader:

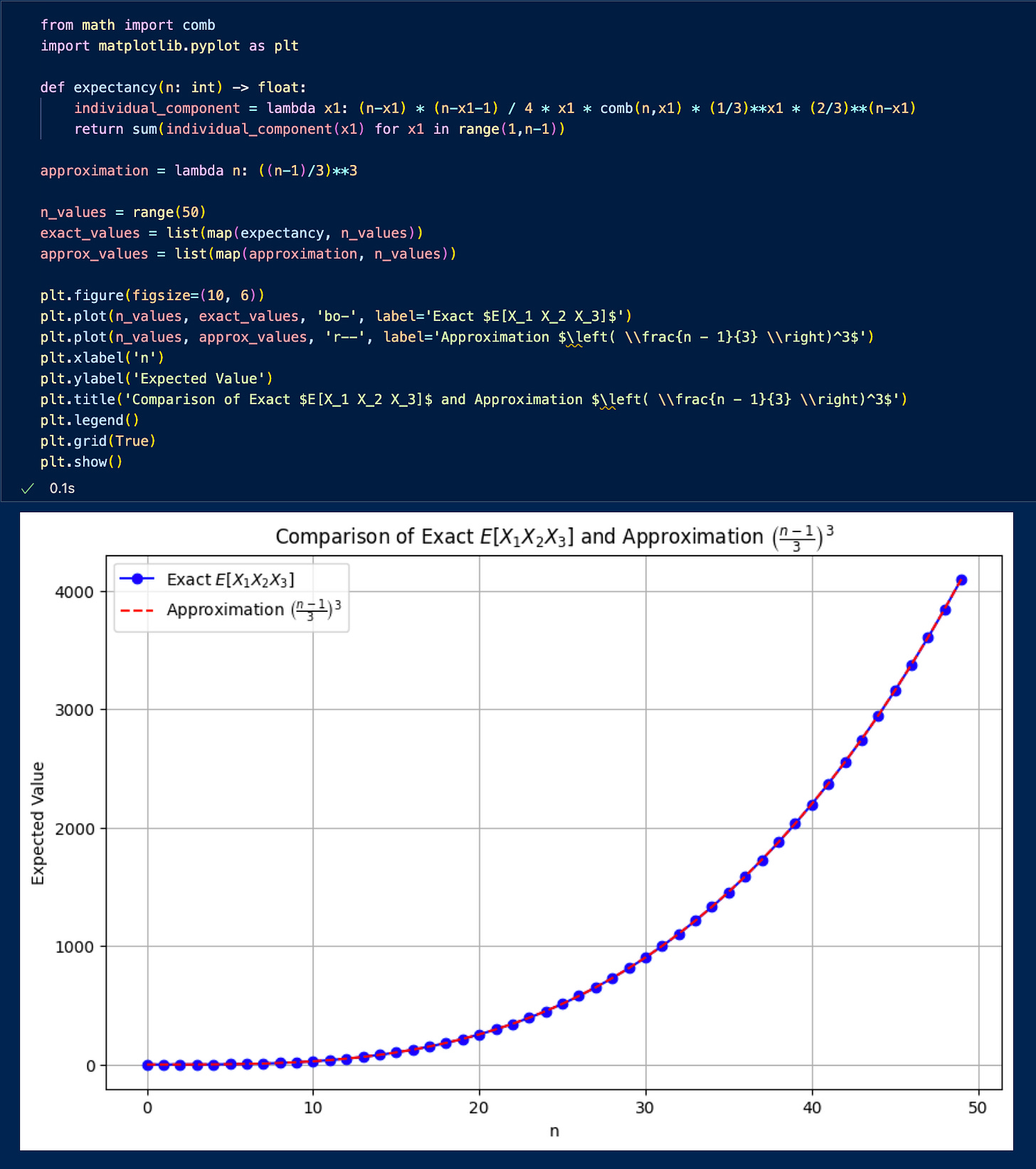
A rather nice approximation emerges:

\(E[X_1 X_2 X_3] \approx \left( \frac{n - 1}{3} \right)^3\)

Perhaps the 2006 Time’s Person of the Year¹ can see why….

1. Wikipedia contributors. “You (Time Person of the Year).” Wikipedia, https://en.wikipedia.org/wiki/You_(Time_Person_of_the_Year).