Discretely Uniform

Approximating dNs and card draws

Have you ever had a problem with a a dN where it would be easier to calculate if it were a uniform distribution? Outside of quant/trader interviews, the answer is probably a hard NO. Nonetheless, I will share my interview ~alpha~ on this blog.

For napkin math approaches to problems (think fast math market making games etc.), we can treat discrete distributions of the form

\(X \sim \{ \text{low},\ \text{low} + \text{step},\ \text{low} + 2\cdot\text{step},\ \dots,\ \text{high} \}\)

as a continuous uniform distribution

\(X \sim \mathrm{Uniform}\bigl( \text{low} - \frac{\text{step}}{2},\ \text{high} + \frac{\text{step}}{2} \bigr)\)

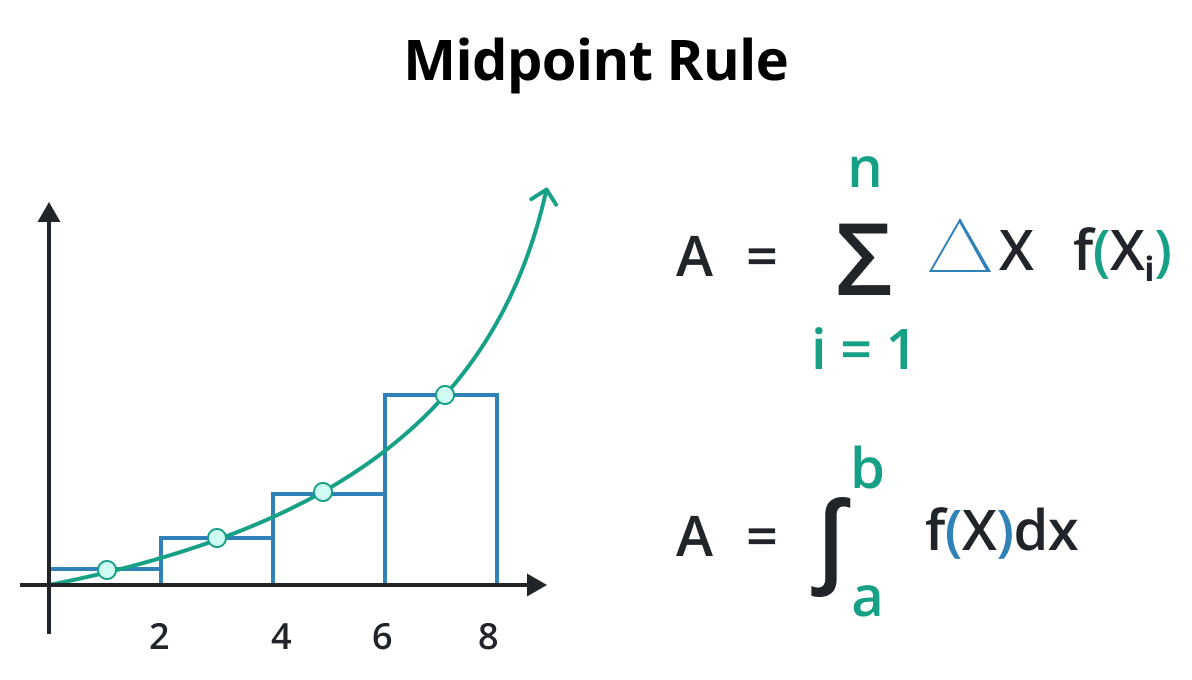
What we’ve essentially done here is treat the discrete value of the original distribution as the center of equally spaced uniform distributions. This preserves the mean of the original distribution and (roughly speaking) the variance as well. The larger the distribution, the more accurately this preserves the variance as the error term is something on the lines of O(1/n^2) where n is the number of discrete outcomes in your original distribution. This is based on the midpoint rule¹ which is a pretty common numerical integration method. In short, you approximate an integral by replacing the curve with rectangles whose heights are measured at the midpoints of subintervals.

Putting it to use

Anyway, let’s actually use this in practice now with a few example questions:

Suppose that you roll a d6 three times, what is the expected value of the minimum of these three rolls?

We can use our midpoint approximation along with k-th ordered statistics to approximate this. For n items drawn from a uniform distribution, we expect the smallest to be 1/(n+1)th of the way along the distribution which gives us:

\(\mathbb{E}\bigl[\min(X_1, X_2, X_3)\bigr] \approx (6.5 - 0.5) \cdot \tfrac{1}{4} + 0.5 = 2\)

And now for the exact:

\(\begin{align*} &\mathbb{E}\bigl[\min(X_1, X_2, X_3)\bigr] \\ &\quad= \sum_{k=1}^{6} k \left[ \left( \frac{7 - k}{6} \right)^3 - \left( \frac{6 - k}{6} \right)^3 \right] \\ &\quad= \frac{1}{216} \sum_{k=1}^{6} k \bigl[ (7 - k)^3 - (6 - k)^3 \bigr] \\ &\quad\approx 2.042 \end{align*}\)

Suppose that we pull out 10 cards (with replacement) from a 52 card deck where A-K is represented as 1-13. What is the fair value of the absolute value of the sum of the 10 cards drawn and 70. In other words, what is the fair value of the 70 strike straddle?

For this, some basic options knowledge comes into play. Recall that the price of an ATM straddle is

\(\text{ATM Straddle} \approx Fe^{-rT}\sqrt{\tfrac{2}{\pi}}\sigma\sqrt{T}\)

We know that the sigma * sqrt(T) * forward component is just the standard deviation, and thus we get:

\(\text{ATM Straddle} \approx \sqrt{\tfrac{2}{\pi}}(\text{std dev}) \approx \tfrac{4}{5}(\text{std dev})\)

Also, recall that the variance of a Uniform distribution:

\(\mathrm{Var}\!\left[X \sim U(a,b)\right] = \frac{(b - a)^2}{12}\)

Alright, now tying together our straddle approximation of 4/5ths of the standard deviation and treating the cards as uniform we get (remember there are approximations in here):

\(\begin{array}{rcl} \mathbb{E}\!\left[ \left| \sum_{i=1}^{10} X_i - 70 \right| \right] & \approx & \dfrac{4}{5} \sqrt{ 10 \cdot \dfrac{(13.5 - 0.5)^2}{12} } \\[10pt] & = & \dfrac{4}{5} \sqrt{ \dfrac{5 \cdot 13^2}{6} } \\[10pt] & = & \dfrac{4}{5} \sqrt{ \dfrac{845}{6} } \approx \dfrac{4}{5}\sqrt{141}\\[10pt] & \approx & \dfrac{4}{5} \cdot 12 \approx 9.6 \\ & \approx & 9.5 \end{array}\)

Note that we rounded down our 9.6 to 9.5 because 4/5 is slightly over sqrt(2/pi) and also the sqrt(141) is a little bit less than 12 (a second reminder that this is a fast math approximation).

And for the actual we have:

\(\begin{align*} &\mathbb{E}\!\left[ \left| \sum_{i=1}^{10} X_i - 70 \right| \right] \\ &\quad= \frac{1}{13^{10}} \sum_{k=10}^{130} \! \left| k - 70 \right| \\ &\qquad \times \sum_{j=0}^{\left\lfloor \frac{k - 10}{13} \right\rfloor} \! (-1)^j \binom{10}{j} \binom{k - 13j - 1}{9} \\ &\quad= \frac{2}{13^{10}} \sum_{k=71}^{130} \! \left( k - 70 \right) \\ &\qquad \times \sum_{j=0}^{\left\lfloor \frac{k - 10}{13} \right\rfloor} \! (-1)^j \binom{10}{j} \binom{k - 13j - 1}{9} \\ &\quad\approx 9.48 \end{align*}\)

Note that we are able to simply the expression due to symmetry. And apologies for the awkward break into multiple lines for those on desktop, but this is the only way I can get it to fit on the mobile screen!

1. https://en.wikipedia.org/wiki/Midpoint_method