Time to get Nifty

settling Indian options

Disclaimer: I am not a financial advisor. I’m a blueberry. I possess no formal financial education, no advanced degrees, and possibly no brain cells. I am merely a moron with a Substack. Absolutely nothing in this article is truthful, factual, or even remotely accurate—it is pure, unfiltered parody. While I will reference various complex concepts, I will simplify them to a level that makes sense to me, which means they will become entirely nonsensical and wrong. Please do not take anything in this article seriously or as advice. I am making all of this up. None of it is true. Not a single word.

I recently wrote a post¹ about how to adjust the time to expiry input of options to account for the final settlement TWAP component (specifically in reference to Deribit’s TWAP terms, but it is worth reading before this to give some additional context and intuition behind the importance of adjusting the time to expiry input in options pricing), and since Indian options are all the rage recently², I figured I’d delve into how to go about the effective time to expiry for the options on those stocks which are settled on a 30 minute VWAP (volume weighted average price).

First and foremost, we’re going to have to have a prior of the distribution of volume of trades in the final 30 minute period. For the sake of both simplicity and to avoid sharing anything proprietary, we will assume that the distribution of volume follows the power law (obviously the exact prior for the distribution would need to be researched):

where there is L time in the VWAP period.

Let t = time to expiry, where 0 <= t <= L. Which means that t = 0 is the expiration and t = L is the instant the VWAP window starts. With t time left inside the window, the random part of the VWAP is:

\(P(t)=\int_{0}^{t} w_{L,k}(s)\,S_{T-s}\,ds\)

Using

\(\operatorname{Cov}[S_{ T−r} ,S_{T−s}]=σ^2 \min(r,s)\)

we obtain Var(P(t)) equals

\(\sigma^{2}\int_{0}^{t}\int_{0}^{t} w_{L,k}(r)w_{L,k}(s)\min(r,s)\;dr\,ds\)

and then carrying out the double integral yields a closed form that is neat in the scaled variable u = t/L

\(\begin{aligned} T_{\text{eff}}^{(\text{in})}(t,k,L)=\, & L\Bigl[ u-\frac{2}{k+2}\bigl(1-(1-u)^{\,k+2}\bigr) \\[6pt] & \quad\;+\frac{1}{2k+3}\bigl(1-(1-u)^{\,2k+3}\bigr) \Bigr] \end{aligned}\)

And just before the window starts (t=L, u=1) that formula reduces to a constant slope value

\(T_{\text{eff}}^{\text{(full window)}}(k,L)= L\Bigl( 1-\frac{2}{k+2}+\frac{1}{2k+3} \Bigr)\)

\(T_{\text{eff}}(t,k,L)= (t-L)\;+\; T_{\text{eff}}^{\text{(full window)}}(k,L)\)

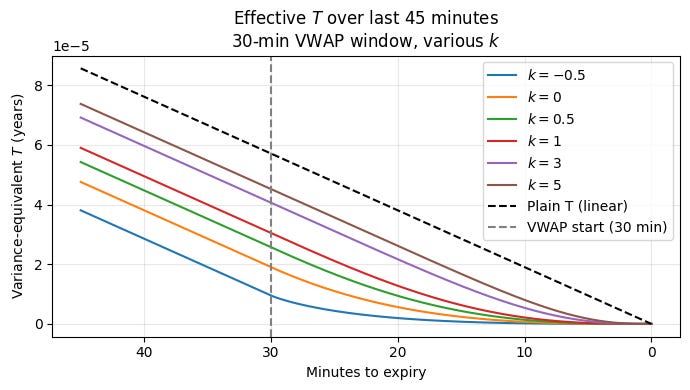
Piecing our cases of being both inside and outside of the window we get:

\(\boxed{% \begin{array}{l} T_{\text{eff}}(t,k,L)=\\[6pt] \begin{cases} (t-L)+L\!\left(1-\frac{2}{k+2}+\frac{1}{2k+3}\right), & t>L,\\[6pt] L\!\Bigl[u-\frac{2}{k+2}\!\left(1-(1-u)^{k+2}\right)\\[4pt] \quad+\frac{1}{2k+3}\!\left(1-(1-u)^{2k+3}\right)\Bigr], & 0\le t\le L, \end{cases}\\[6pt] u=\dfrac{t}{L} \end{array}}%\)

Two important things to note:

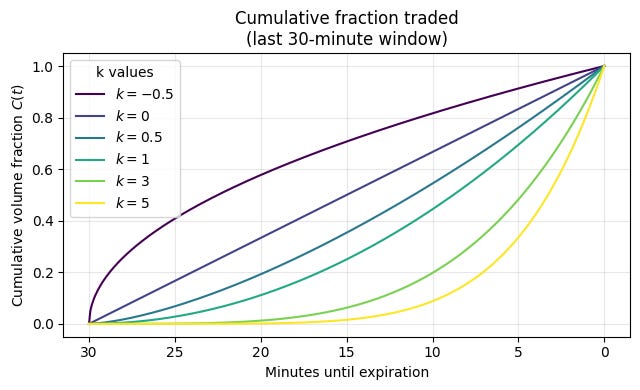
1. k = 0 reproduces TWAP as uniform distribution of volume is the same as just weighting by time.

2. As k tends to infinity, the effective time to expiration approaches t since if all of the weight is at the last possible moment, the underlying has the full window period to drift before settlement.

And lastly, a quick visual aide:

1. Semet, Evan. “Back to the Futures.” Bits, Bytes, and Bets, Substack, https://bitsbytesandbets.substack.com/p/back-to-the-futures

2. Bloomberg News. “Jane Street’s $1 Billion Trade Puts Spotlight on Indian Options.” Bloomberg, https://www.bloomberg.com/news/articles/2024-04-22/jane-street-s-1-billion-trade-puts-spotlight-on-indian-options?embedded-checkout=true