Disclaimer: I am not a financial advisor. I’m a blueberry. I possess no formal financial education, no advanced degrees, and possibly no brain cells. I am merely a moron with a Substack. Absolutely nothing in this article is truthful, factual, or even remotely accurate—it is pure, unfiltered parody. While I will reference various complex concepts, I will simplify them to a level that makes sense to me, which means they will become entirely nonsensical and wrong. Please do not take anything in this article seriously or as advice. I am making all of this up. None of it is true. Not a single word.
Let’s start with a pretty basic options trivia question.
Question: How can we be long both gamma and theta?
Well, I think generally speaking, an interviewer is probably trying to ask you about skew if you get this question—although there is another answer we’ll get to afterwards.
Take this vol surface with put skew for example. If we sell a put at -1 NS and long a call at +1 NS then we should have a position that is net long both gamma and theta. To intuitively see why this is the case, the option’s premium has to be higher for higher implied vol and since there is the same time to expiry, the added premium must decay out over the same time period meaning that the put has strictly higher theta than the call. As for the gamma component, higher implied vol widens the implied distribution of the underlying, thus making the convexity of the price less sensitive to local movements; therefore, the call has more gamma than the put.
Side Note: NS stands for Normalized Strike. It converts Strikes into a Z-score to better normalize your surfaces.
Now, let’s talk about the other answer that I mentioned before: deep ITM puts. All options have positive gamma. So the long gamma box is checked off already. Let’s go on a brief tangent and talk about a future roll for a second. Suppose that we have a future roll with the long leg being spot and the short leg being the front month future. Come expiration, the value of the future should converge to spot right? So (assuming constant interest rates), we expect the price of this future roll to “decay” over time right? The answer to both of those questions is yes if you couldn’t already tell. Well TLDR, conditioned on nothing happening, we expect the future to converge to spot, so the puts should become more in the money (emphasis on the conditioned on nothing else happening part). If the put is deep enough in the money, the “gain” we get from the roll component will outweigh the decay of the premium thus leading to a net positive theta of the option.
Notice how the first term for theta is the same for both calls and puts. It is the second (rate) term that differs. Let’s break this up into “premium decay” and “rate decay” and plot this out. We’ll use the following constant values (we’re using a flat vol surface here):
I added regular strike on the top but NS is the only space I really think about in.
Anyway, I think that the important thing for options traders is to be able to pinpoint where your PnL is coming from; just saying you’re ‘bleeding theta’ isn’t good enough. What if you were ‘bleeding’ because of an inappropriate implied interest rate for the product? That is fundamentally different from the vol premium peeling off, hence the need to separate it out. Better risk breakdown let’s you better calculate what to hedge with. Maybe future rolls would eliminate some unwanted risk? Idk it depends on the position obviously, but you can’t make optimal decisions with suboptimal information.



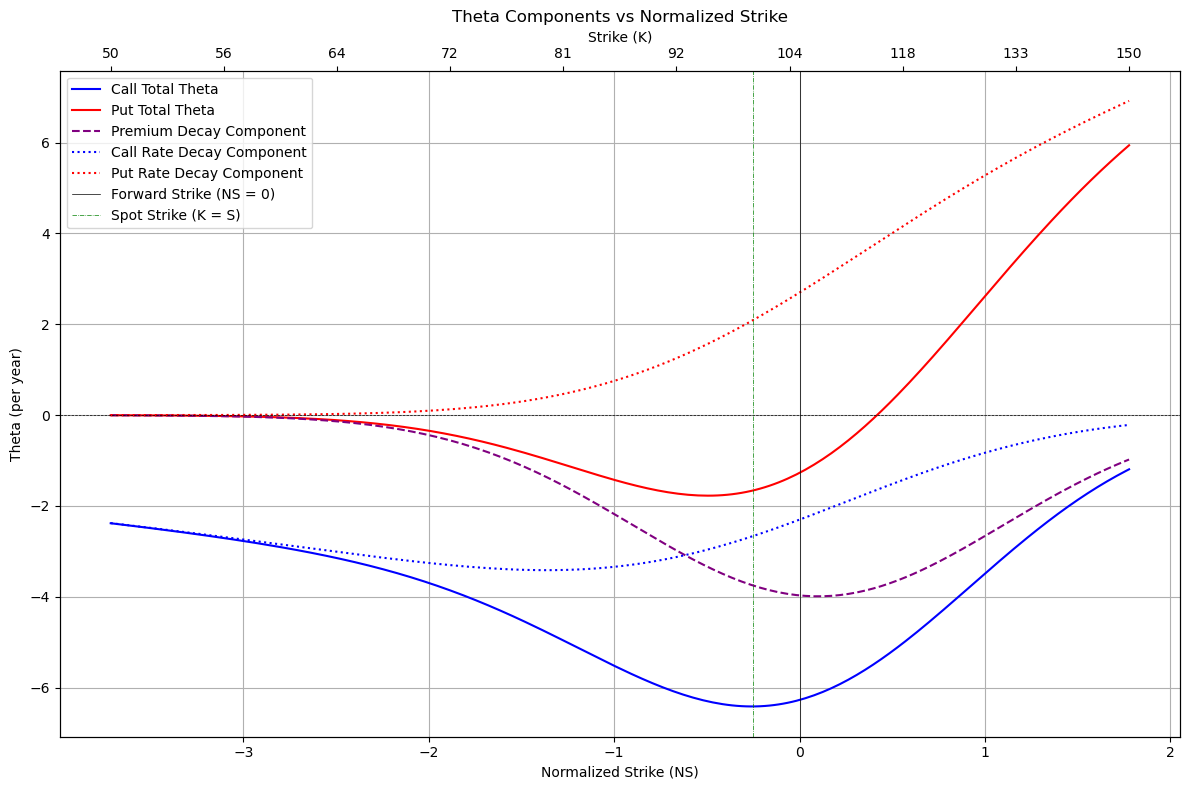
Drilling down on theta bleed sources is a huge chunk of research effort at a lot of the larger MMs. I have spent a decent amount of time on it personally. Not fun but incredibly important